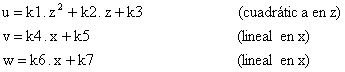
Deformaciones longitudinales especificas en las tres direcciones:
Se calculan derivando las hipotesis de corrimiento:
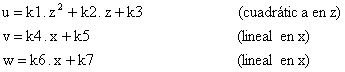
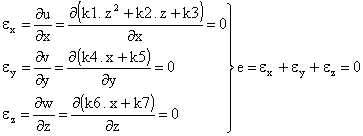
Ecuaciones de Equilibrio Interno (E.E.I.) en deformaciones
Las ecuaciones de equilibrio interno en deformaciones son:
Siendo 
(dilatación cúbica: en un
determinado punto la suma de las deformaciones ex, ey, ez es siempre el mismo
valor e).
Como u, v, y w son lineales respecto a x, y, y z respectivamente, sus Laplacianos son:
Eliminando los terminos nulos, queda:
2 . k1 . G =
0, las cual no se verifica, porque aunque e es nula, y los laplacianos de los
corrimientos v y w son nulos, el laplaciano del corrimiento u es distinto de
cero, por lo tanto k1 también lo es.
Ecuaciones de Equilibrio en el Contorno (E.E.C.) en deformaciones
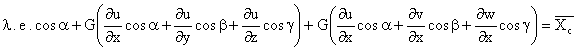
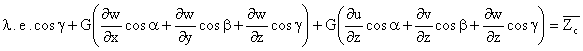
Y eliminando los terminos nulos,
queda:
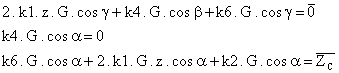
Las cuales no se verifican, porque no se cumple la segunda ecuación, ya que por hipotesis de corrimientos k4 es distinto de cero.
Ecuaciones De Compatibilidad (E.D.C.) en deformaciones
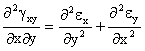
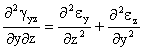
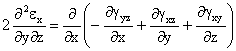
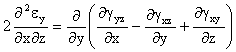
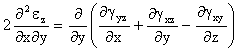
Al ser nulas todas las deformaciones tanto longitudinales como angulares, las derivadas también lo son, verificandose las ecuaciones de compatibilidad.
Conclusión:
Concluimos que para el problema de flexión simple (sin considerar el peso propio), la solución en terminos de corrimientos brindada por la Resistencia de Materiales no es aceptable, ya que lo hemos comprobado mediante la teoría de la elasticidad.