Deformaciones longitudinales especificas en las tres direcciones:
Se calculan derivando las hipótesis de corrimiento:
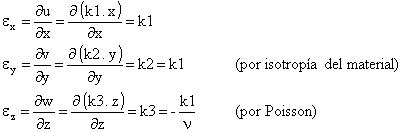
Ecuaciones de Equilibrio Interno (E.E.I.) en deformaciones
Las ecuaciones de equilibrio interno en deformaciones son:
Siendo 
(dilatación cúbica: en un
determinado punto la suma de las deformaciones ex, ey, ez es siempre el mismo
valor e).
Como u, v, y w son lineales respecto a x, y, y z respectivamente, sus Laplacianos son:
Las cuales se cumplen, ya que e es
una constante y además los Laplacianos de los corrimientos son todos nulos al
igual que las fuerzas másicas.
Ecuaciones de Equilibrio en el Contorno (E.E.C.) en deformaciones
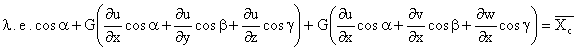
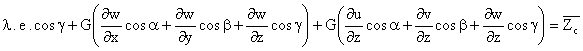
Teniendo en cuenta lo siguinete:
Y eliminando los terminos nulos,
queda:
Cara 5:
Cara 6:
Ya que la constante k1 es igual para ambas caras, se verifican las ecuaciones de equilibrio en el contorno.
Ecuaciones De Compatibilidad (E.D.C.) en deformaciones
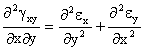
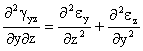
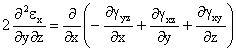
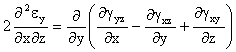
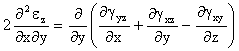
Al ser nulos todos las deformaciones angulares y las derivadas segundas de las deformaciones longitudinales respecto a cualquiera de las tres variables, se verifican las ecuaciones de compatibilidad.
Conclusión:
Concluimos que para el problema de compresión simple (sin peso propio), la solución en terminos de corrimientos brindada por la Resistencia de Materiales es aceptable, ya que la hemos verificado mediante la teoría de la elasticidad.