Se deben verificar las: E.E.I., E.E.C. y E.D.C como condición necesaria y suficiente (Teorema de la unicidad de la solución elástica).
Verificación de las Ecuaciones de
Equilibrio Interno (E.E.I.
Las ecuaciones a verificar
son:
![]() txy = tyx
txy = tyx
![]() txz = tzx
txz = tzx
Las tensiones tangenciales se igualan de a pares por el Principio de reciprocidad de las tensiones.
Eliminando los terminos nulos, nos
queda:
![]()
![]() (porque ambas
no dependen de Z y su derivada es nula)
(porque ambas
no dependen de Z y su derivada es nula)
![]() Verifica
Verifica
Cara 5 y 6
![]()
![]()
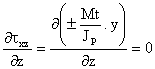 Verifica
Verifica
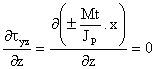 Verifica
Verifica
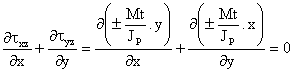 Verifica
Verifica
Por lo tanto se verifican las ecuaciones de equilibrio interno en tensiones.
Verificación de las Ecuaciones de
Equilibrio en el Contorno (E.E.C.
Las ecuaciones a verificar
son:
![]()
![]()
Construimos la siguiente tabla, la que para este caso no es tan necesaria ya que el prisma estudiado es de geometría regular, pero para geometrías irregulares y complicadas es una buena manera de representar el sólido estudiado y reduce las posibilidades de error.
|
Cara |
GEOMETRIA |
FUERZAS DE
CONTORNO | |||||||
|
cos a |
cos b |
cos g |
X |
Y |
Z |
Xc |
Yc |
Zc | |
|
1 |
1 |
0 |
0 |
a/2 |
-b/2 £ y £ b/2 |
0 £ z £ h |
0 |
0 |
0 |
|
2 |
-1 |
0 |
0 |
-a/2
|
-b/2 £ y £ b/2 |
0 £ z £ h |
0 |
0 |
0 |
|
3 |
0 |
1 |
0 |
-a/2 £ x £ a/2 |
b/2 |
0 £ z £ h |
0 |
0 |
0 |
|
4 |
0 |
-1 |
0 |
-a/2 £ x £ a/2 |
-b/2 |
0 £ z £ h |
0 |
0 |
0 |
|
5 |
0 |
0 |
1 |
-a/2 £ x £ a/2 |
-b/2 £ y £ b/2 |
Z |
-Mt.y/JP |
Mt.y/JP |
0 |
|
6 |
0 |
0 |
-1 |
-a/2 £ x £ a/2 |
-b/2 £ y £ b/2 |
0 |
Mt.y/JP |
-Mt.y/JP |
0 |
Eliminamos los terminos nulos:
![]()
![]()
Cara 1, 2, 3, 4: cos g = 0
![]() Verifica
Verifica
Cara 1:
![]() No
Verifica
No
Verifica
Cara 2:
![]() No
Verifica
No
Verifica
Cara 3:
![]() No
Verifica
No
Verifica
Cara 4:
![]() No
Verifica
No
Verifica
Cara 5:
![]() Verifica
Verifica
![]() Verifica
Verifica
![]() Verifica
Verifica
Cara 6:
![]() Verifica
Verifica
![]() Verifica
Verifica
Verificación de las Ecuaciones De
Compatibilidad
Utilizaremos las ecuaciones de
Beltrami (debido a que Xm=Ym= 0 y
Zm = - Pe, es una constante)
![]()
![]()
![]()
![]()
donde n = Coeficiente de
Poisson.
Siendo ![]() (tensión cúbica:
en un determinado punto la suma de las tensiones sx, sy, sz es siempre el mismo
valor s).
(tensión cúbica:
en un determinado punto la suma de las tensiones sx, sy, sz es siempre el mismo
valor s).
Recordando que
![]()
Dado que tzx = f(y) lineal
que tzy = f(x) lineal
Las primeras derivadas dan cte ó cero, y las segundas derivadas son todas nulas. Verifican las ecuaciones de compatibilidad.
Conclusión:
Concluimos que para el problema de torsión simple (sin considerar el peso propio), la solución tensional brindada por la Resistencia de Materiales no es aceptable, ya que la hemos verificado mediante la teoría de la elasticidad.
Lo estudiado en Resistencia de Materiales, se cumple para el caso de Compresión Simple y Flexión Simple, pero no se cumple para Torsión Simple, ya que las tensiones no son proporcionales a la distancia radial, como explica la Resistencia de Materiales.