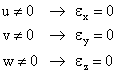
Principal Torsión simple Atrás
Hipótesis de
corrimientos
Para llegar al estado tensional, Saint Venant partió de las hipótesis de corrimientos:
Las proyecciones horizontales de las secciones rotan pero no se deforman:
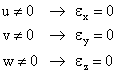
Las secciones se alabean, pero si tomamos una fibra imaginaria cualquiera, su longitud no varia, entonces según z, la deformación ez es nula, pero existe corrimiento w.
Los corrimientos w son f(x;y), y no de z, pues para un punto (x;y) dado, todos los puntos de coordenadas (x;y) tienen el mismo corrimiento en las distintas secciones.
![]()
Consideramos la sección genérica de la figura de abajo, para analizar los corrimientos u y v en función de las coordenadas del punto.
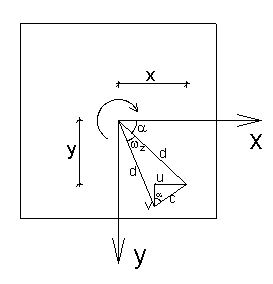
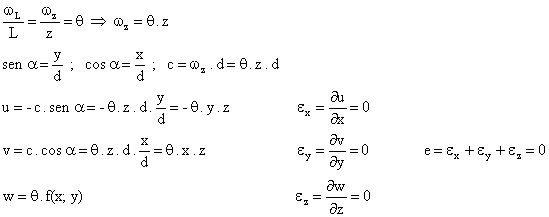
Hipótesis de fuerzas de
masa
En este caso se desprecia el peso
propio, por lo tanto no existirán fuerzas másicas de ningún
tipo:
Xm = Ym =
Zm = 0
Hipótesis de fuerzas de contorno
|
Cara 1, 2, 3, 4:
|
Cara 5:
|
Cara 6:
|
Siguiente