
Cálculo de deformaciones y corrimientos

Los corrimientos los obtenemos como sigue:
Integrando 3 :
![]()
Reemplazando 11 en 5 :
![]()
Integrando 13 :
![]()
Reemplazando 12 en 6 :
![]()
Integrando 17 :
![]()
Reemplazando 16 y 19 en 4 :
![]()
Para que 21 se cumpla para todo z:
![]()
Reemplazando 15 en 1 :
![]()
Entonces:
![]()
Integrando 25 :
![]()
Reemplazando 20 en 2 :
![]()
Entonces:
![]()
Integrando 29 :
![]()
Reemplazando 27 y 31 en 23 :
![]()
Integrando 32 respecto de y:
![]()
Integrando 32 respecto de x:
![]()
Integrando 24 respecto de x:
![]()
Integrando 28 respecto de y:
![]()
Componemos F1(x,y), a partir de 36 y 38 :
![]()
Derivando 35 respecto de y:
![]()
Derivando 37 respecto de x:
![]()
Reemplazando 40 y 41 en 39 :
![]()
Resumiendo:
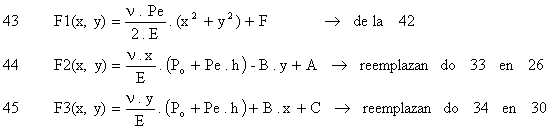
Y los corrimientos son:

Las constantes se determinan fijando las coordenadas de un punto que no se desplace ni gire en ninguna dirección, de la forma siguiente:
En el punto de coordenadas x = y = z = 0, los corrimientos
valen: u = v = w = 0 ![]()
En el punto de coordenadas x = y
= z = 0, los giros valen: ![]() , tomando
, tomando 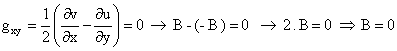
Si tomamos los 2 giros restantes, observamos que quedan igualdades del tipo: 0 = 0
Las expresiones finales de los corrimientos:
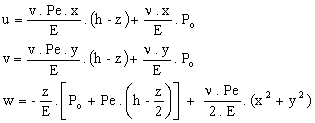
Como estos corrimientos fueron obtenidos a partir de las hipótesis de tensiones, estos verifican las E.E.I., las E.E.C. y las E.D.C., ya que las tensiones las verifican.