Principal Flexión simple Atrás
MODELACIÓN EN SAP:
Primero seleccionamos las unidades con las cuales trabajaremos (kgf, cm, C).
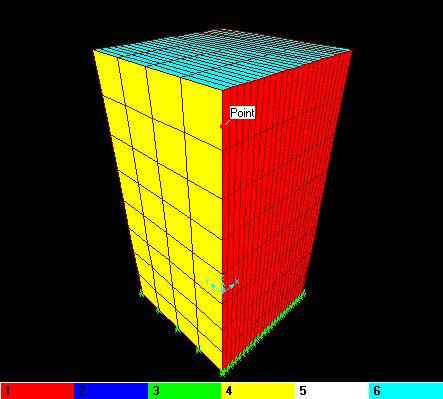
Geometría: Al igual que en la aplicación numérica el sólido tiene las siguientes dimensiones a = 50 cm, b = 50 cm y h = 100 cm.
El prisma se ha discretizado de tal manera que cada elemento sólido que lo compone tenga sus tres lados de: 2,0833 cm, 12,5 cm, y 12,5 cm en x, y, y z respectivamente, es decir 24 divisiones en x, 4 divisiones en y, y 8 divisiones en z.

Código de colores de
las caras.
Materiales: definimos de que material será el sólido (Cobre), y cada una de sus propiedades (E, n), teniendo en cuenta que en este caso se desprecia la influencia del peso propio.
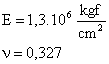
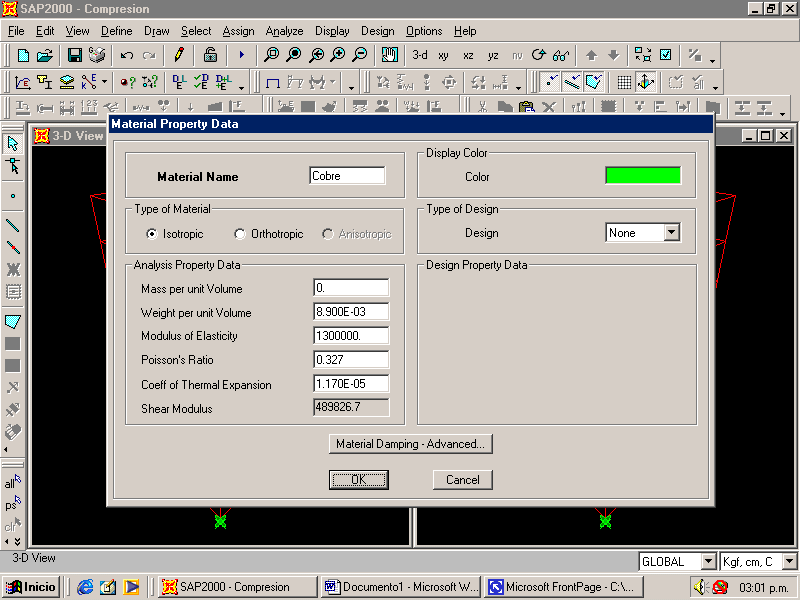
En esta figura se
muestra el material que hemos adoptado.
Condiciones de vinculo: en el plano de cota z = 0, es donde colocaremos las restricciones en cada uno de los nodos, a todos ellos se le restringe el movimiento en la dirección de z (es decir w), y tambien la posibilidad de girar en torno a cualquiera de los tres ejes, al punto de coordenadas (0;0;0) se le restringen los movimientos en las tres direcciones x, y, z (es decir u, v, w), ademas de las rotaciones en torno a los tres ejes, a los puntos de coordenadas (-25;0;0) y (25;0;0) se le restringe además el movimiento en la dirección de y, esto es así debido a que el cuerpo tiende a girar.
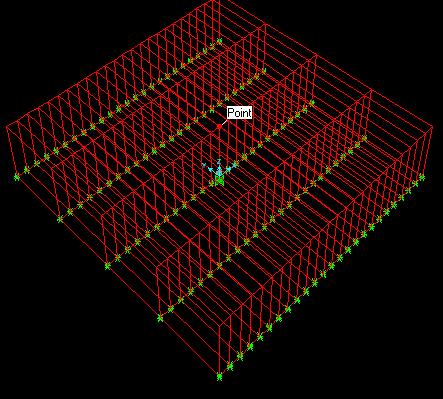
Detalle de apoyos en la cara 5.
Cargas: antes de asignarle algún tipo de carga al sólido, definimos un estado de carga, como se muestra en la figura:
En la figura anterior se muestra el estado de carga y se observa que el multiplicador de peso propio es cero (no se considera).
Se le coloca una carga por unidad de superficie en la cara 6 (en SAP la de arriba) de valor:
|
Coordenada x (cm) |
Tensión (kgf/cm2) |
Tramo |
Tensión media (kgf/cm2) | ||
|
N° |
Coord.
Inicial (cm) |
Coord.
Final (cm) | |||
|
-25 |
-1,6 |
1 |
-25 |
-22,917 |
-1,533 |
|
-22,917 |
-1,467 |
2 |
-22,917 |
-20,833 |
-1,400 |
|
-20,833 |
-1,333 |
3 |
-20,833 |
-18,750 |
-1,267 |
|
-18,750 |
-1,200 |
4 |
-18,750 |
-16,667 |
-1,133 |
|
-16,667 |
-1,067 |
5 |
-16,667 |
-14,583 |
-1,000 |
|
-14,583 |
-0,933 |
6 |
-14,583 |
-12,500 |
-0,867 |
|
-12,500 |
-0,800 |
7 |
-12,500 |
-10,417 |
-0,733 |
|
-10,417 |
-0,667 |
8 |
-10,417 |
-8,333 |
-0,600 |
|
-8,333 |
-0,533 |
9 |
-8,333 |
-6,250 |
-0,467 |
|
-6,250 |
-0,400 |
10 |
-6,250 |
-4,167 |
-0,333 |
|
-4,167 |
-0,267 |
11 |
-4,167 |
-2,083 |
-0,200 |
|
-2,083 |
-0,133 |
12 |
-2,083 |
0,000 |
-0,067 |
|
0 |
0 |
13 |
--- |
--- |
--- |
|
2,083 |
0,133 |
14 |
2,083 |
0,000 |
0,067 |
|
4,167 |
0,267 |
15 |
4,167 |
2,083 |
0,200 |
|
6,250 |
0,400 |
16 |
6,250 |
4,167 |
0,333 |
|
8,333 |
0,533 |
17 |
8,333 |
6,250 |
0,467 |
|
10,417 |
0,667 |
18 |
10,417 |
8,333 |
0,600 |
|
12,500 |
0,800 |
19 |
12,500 |
10,417 |
0,733 |
|
14,583 |
0,933 |
20 |
14,583 |
12,500 |
0,867 |
|
16,667 |
1,067 |
21 |
16,667 |
14,583 |
1,000 |
|
18,750 |
1,200 |
22 |
18,750 |
16,667 |
1,133 |
|
20,833 |
1,333 |
23 |
20,833 |
18,750 |
1,267 |
|
22,917 |
1,467 |
24 |
22,917 |
20,833 |
1,400 |
|
25 |
1,6 |
25 |
25,000 |
22,917 |
1,533 |
y de signo positivo lo que significa que esta dirigida hacia el interior del sólido (compresión).
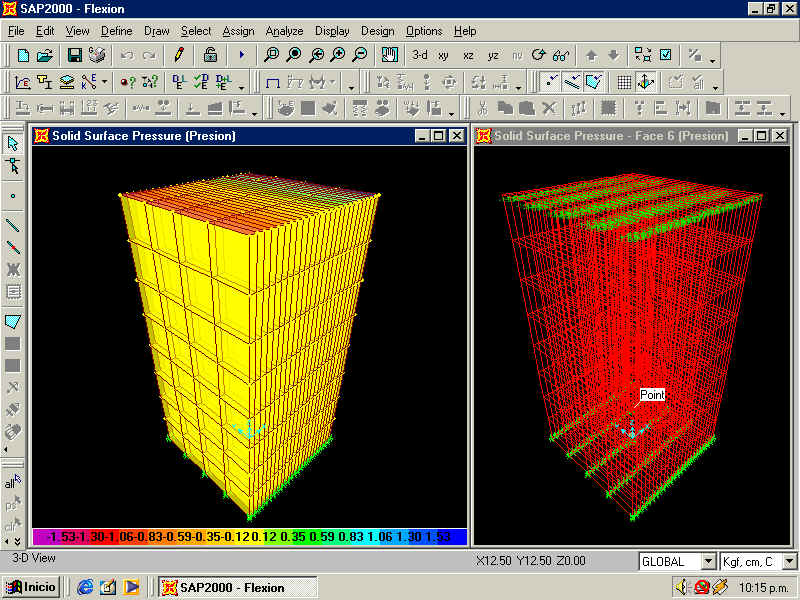
Figura donde se
muestran las cargas actuantes, y se observa la variación lineal de la carga
respecto de x.
Habiendo ingresado estos datos se
procede a correr el programa y evaluar los resultados obtenidos.
Corrimientos: 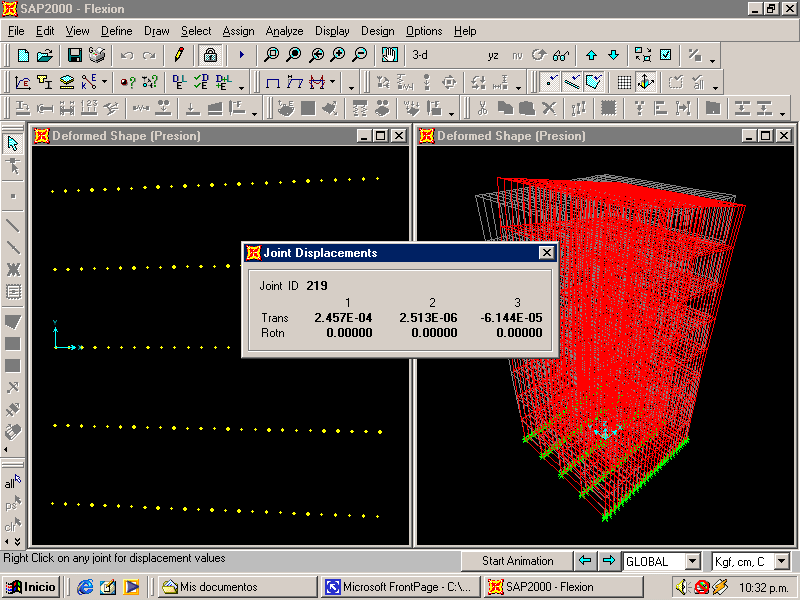
En la figura anterior
se muestran los corrimientos del punto A; 1, 2, 3, equibalen a x, y, z
respectivamente.
Tensiones:
Las tensiones s11 = s22 = t12 = t13 = t23 = 0.
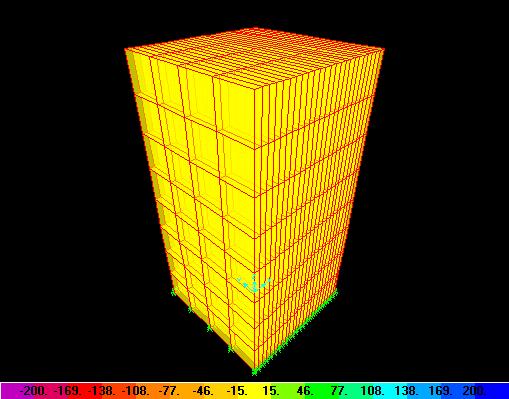
El color amarillo
equivale a un valor de tensión igual a 0 kgf/cm2.
y la tensión s33 varia linealmente respecto de x, como se ve en la figura siguiente:
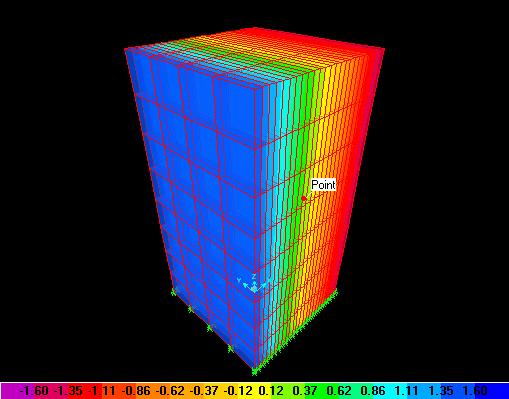
El menor valor de
sz = -1,6 kgf/cm2 esta en rosado,
y el valor maximo de sz = 1,6
kgf/cm2 esta en azul.
Reacciones:
|
Coordenada x (cm) |
Reacción para y = 25
cm (kgf) |
Reacción para y = 12,5
cm (kgf) |
|
-25 |
-10,11 |
-20,21 |
|
-22,917 |
-19,07 |
-38,14 |
|
-20,833 |
-17,33 |
-34,65 |
|
-18,750 |
-15,60 |
-31,20 |
|
-16,667 |
-13,86 |
-27,73 |
|
-14,583 |
-12,13 |
-24,26 |
|
-12,500 |
-10,40 |
-20,80 |
|
-10,417 |
-8,67 |
-17,33 |
|
-8,333 |
-6,93 |
-13,86 |
|
-6,250 |
-5,20 |
-10,40 |
|
-4,167 |
-3,47 |
-6,93 |
|
-2,083 |
-1,73 |
-3,47 |
|
0 |
0 |
0 |
|
2,083 |
1,73 |
3,47 |
|
4,167 |
3,47 |
6,93 |
|
6,250 |
5,20 |
10,40 |
|
8,333 |
6,93 |
13,86 |
|
10,417 |
8,67 |
17,33 |
|
12,500 |
10,40 |
20,80 |
|
14,583 |
12,13 |
24,26 |
|
16,667 |
13,86 |
27,73 |
|
18,750 |
15,60 |
31,20 |
|
20,833 |
17,33 |
34,65 |
|
22,917 |
19,07 |
38,14 |
|
25 |
10,11 |
20,21 |
A fin de comparar los valores obtenidos analíticamente se confeccionna la tabla siguiente:
|
Puntos |
u |
v |
w |
sz
(kgf/cm2) |
|
A:
(12,5;12,5;100) |
2,457.10-4 |
2,513.10-6 |
-6,144.10-5 |
--- |
|
Sección de
abcisa x = 25 cm |
--- |
--- |
--- |
-1,60 |
Los puntos A, B, C y D son los mismos puntos que se tomaron el la aplicación numérica.